このような違いはどこから来るのでしょうか。これを説明する前に、物質の導電率σ [S/cm]が、電子の電荷e[C]、キャリア密度n [cm-3]と移動度μ [cm2/Vs]のを使って、 σ=neμ (1)
で表されることを知っておく必要があります。(この式の導き方は解説をお読み下さい) 金属におけるσの温度変化は、キャリア密度nが一定なので移動度で決まり、温度上昇とともに、格子振動によって移動度?が小さくなることが原因であるとされます。 一方、半導体ではnは数桁にわたって変化します。それは、純粋の半導体(真性半導体)のキャリア密度nは、温度T[K]に対して、 n=n0exp(-Eg/2kT) (2)
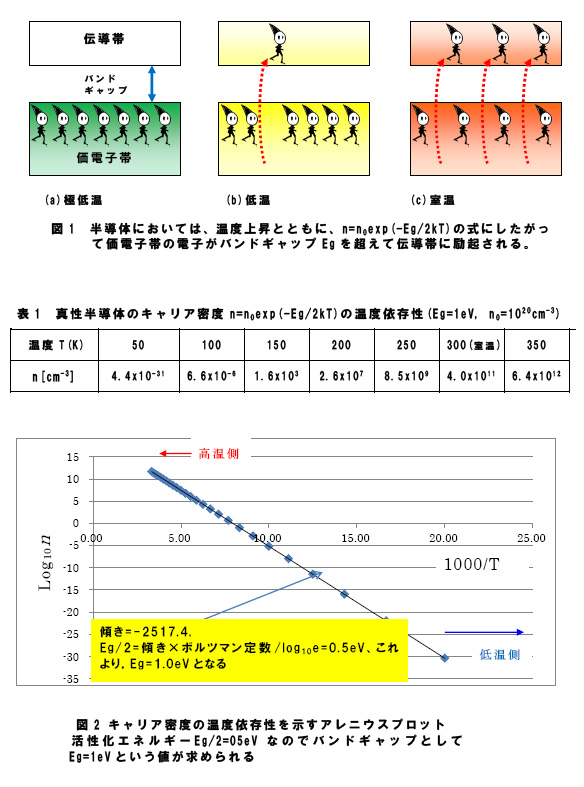
の形で指数関数的に変化するからです。ここに、n0は定数、Egはバンドギャップの大きさ、kはボルツマン定数です。この式は、図1に模式的に示すように、価電子帯の電子が熱的にバンドギャップEgを超えて伝導帯に励起されるようすを表したものです。
【250度温度が上がると42桁も電子が増える】
表1に、nがTとともにどのように変化するかをEg=1eV, n0=1020[cm-3]の場合に示します。キャリア密度は50Kから室温(300K)のあいだになんと42桁も変化するのです。
式(2)の常用対数をとると キャリア密度の常用対数を温度の逆数1/Tに対して描くと直線になります。このグラフをアレニウスプロットといい、図2に示すように傾きからバンドギャップが求められます。
要点Check: